Models of Learning

• Introduction

  1. Task description

• Reinforcement Learning

  1. Theory
     • Rescorla-Wagner
     • SoftMax
  2. Data plotting
  3. Simulation
     • Example participants
     • More participants
     • Explore Parameters
     • Grid Search
     • Marginal distributions
     • Summary values
  4. Real data
     • Fit the data
     • Statistical inference
  5. Review
     • Modelling how-to

• Bayesian Learning

  1. Coin tossing
     • Probability
     • Likelihood
     • Uncertainty
     • Learning
     • Review
  2. Bandit task
     • Updating
     • Transition function
     • Learning rate

Developed by
Jill O'Reilly
Hanneke den Ouden
-August 2015

The Observation Equation

At the beginning of each trial, you then need to decide based on these 2 values, which machine you are going to pick. You could:

• Always pick the stimulus with the highest value
• Or sometimes also explore whether the other machine got better.

It turns out that even though the first option would lead to most reward in this particular task, humans and animals don't usually use this strategy of 'probability maximising' (i.e. picking the simulus with the highest probability of reward). Rather they pick the stimulus with the highest probability more, but not all the time. However, they differ in quite how much you let the probabilities determine your choice. To model how subjects translate the learned values into a choice, we will use a model that can capture these different strategies. For this, we use the so-called soft-max equation:

Observation Equation (softmax)

Let's have a look at the effect of beta on the choice probability.

Assume there are 2 stimuli A and B, where the value of B is always [1-value A].

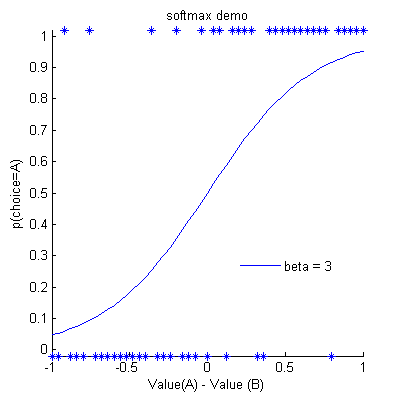
In the plot below, we used an example beta of 3, and plotted both the value of A against the probability of choosing A:

Softmax function

• The probability of choosing stimulus A increases monotonically with the difference in value for A versus B.
• The asterisks mark choices that the subject made based on these choice probabilities, and you can see that the subject chooses A most of the time when V_A > vB_B, but not always.
• This is where the term 'softmax' comes from: the subject picks the stimulus with the maximum value most of the time, so it's a 'soft' maximising function

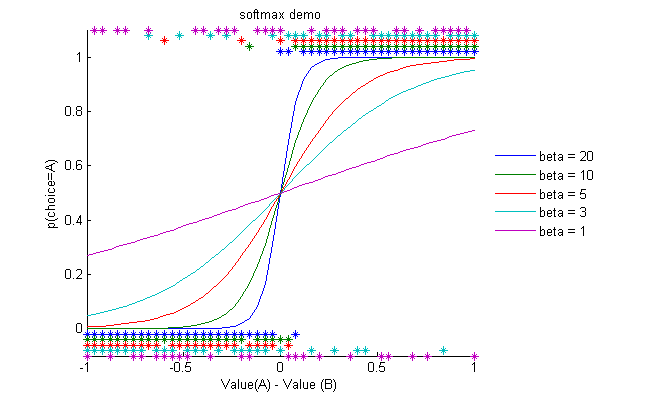
How does the softmax function change when we change the value of β?

?

Effect of different values of β

• A larger β means that choices become more 'deterministic', i.e. you are more likely to pick the option with the highest value
• When β is smaller, you become more 'exploratory', i.e. you are more likely to pick the other option now and again as well.

OPTIONAL: EXPLORING THE SOFTMAX FUNCTION

If you would like, you can explore the softmax function behaviour a little bit more, using the RL_tutorial_softmaxDemo.m code in the ReinfLearn folder. You can simply open the file, change the values of beta, save, and press 'run' to get the plots above.

Here are a few questions to pique your interest

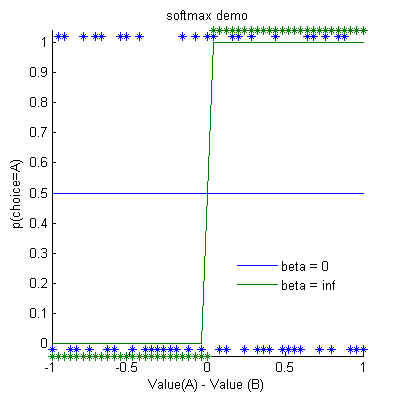
• What happens when the value of the softmax β is 0?
  What if β is infinite?

  ?

  Extreme values of β

  

  • When β = 0, the choice probability is not affected by the value of the stimuli and always exactly at chance level.

  • When β = ∞, choices become completely deterministic and the subject always picks the option with the maximum value.
    

  Mathematically:

  • When β = 0, the values don't matter as they are multiplied by 0

    

  • When β = ∞,

    

    • So if V_A >V_B, even if this difference is tiny, then exp(∞ x V_A))>> exp(∞ x V_B), and so p(A)=1,
    • vice versa when V_B > V_A.

• Can you work out why a negative value for β doesn't make sense?

  ?

  Because that would mean the subject would be more likely to pick the stimulus that has the lowest value! Now that would be a little silly...

►►►